diario de César el mundo matemático de 1 bach: CLASE 6 NOVIEMBRE

domingo, 8 de noviembre de 2015

CLASE 6 NOVIEMBRE

Hoy en clase hemos continuado con la factorización, lo primero que hemos hecho es resolver el polinomio que no terminé en la anterior entrada:

que aquí nos quedamos, pues la resolución es la siguiente:

ahora tenemos dos ecuaciones de 2 grado por lo que buscaremos si tienen solución real:

1) $x=\frac{-2\pm \sqrt[2]{2^2-4\cdot{1}\cdot{2}}}{2}$ no tiene solución real.

2) $x=\frac{2\pm \sqrt[2]{-2^2-4\cdot{1}\cdot{2}}}{2}$ tampoco tiene solución real.

Por lo que la factorización se quedaría así:

Volviendo a lo de clase nos planteó este ejercicio: factorizar el polinomio:

y nos puede venir a la idea de usar las ecuaciones bicuadradas sustituyendo x4 y x2 por t2 y t respectivamente, pues haciendolo he llegado a la conclusión de que esta ecuación no tiene solución real. Por lo que queremos (al observar el polinomio) ver el polinomio como un cuadrado:

entonces llegamos a la conclusión de que: This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Factorizar: This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

podemos resolver: This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

y ahora teniendo el 2 vamos a dividir p(x) entre This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

no podemos hacer ruffini por lo que el resultado ya os lo pongo yo, C(x)= This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

y se factorizaría como el anterior ya que el resultado es el mismo.

Factorizar: This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

vemos cuales son los divisores de el término independiente que son: +/-1, +/-2, +/-3, +/-6 y tras minutos haciendo ruffini obrservo que P(x) no tiene raices enteras. Es cuando nos planteamos: ¿y si buscamos raíces racionales?
Para buscarlas necesitamos esta proposición: raíces racionales de un polinomio con coeficientes enteros: p(x)=

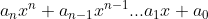
siendo an y a0 distintos de 0. siendo $p(x)\in$ entonces si c/d (fracción irreducible) es raíz racional de P(x) --> c/a0 y d/an es decir que c sea divisor de an y d sea divisor de a0. Entonces This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

divisores de an= +/- 1, +/-2, +/-3, +/-5, +/-6, +/-10, +/-15, +/-30 y divisores de a0= +/-1, +/-2, +/-3, +/-6 probamos con el más pequeño en ruffini:

	30 -13 -13 +6

	15 1 -6
1/2	30 2 12 0

Y nos queda: This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

y resolvemos la ecuación de 2 grado y nos salen estas 2 soluciones: x1=-2/3 x2= 3/5 y la factorización sería: P(x)=30 (x-1/2)(x+2/3)(x-3/5)

diario de César
el mundo matemático de 1 bach

domingo, 8 de noviembre de 2015

CLASE 6 NOVIEMBRE

No hay comentarios:

Publicar un comentario