REFLEXIÓN METRÓNOMOS

Nuestro profesor nos ha propuesto una actividad que en este caso habla de metrónomos y nos pide que observemos esto como una metáfora... 

Los metrónomos empiezan con movimientos totalmente diferentes pero con la trasmisión de energía los 32 metrónomos acaban con el mismo movimiento.

En mi punto de vista, tras ver otros blogs de mis compañeros, llevándolo a un ámbito social o incluso de la clase o de la propia vida... no estaría bien el que todos acabemos haciendo lo mismo ya que la gente dejaría de pensar por si mismos y de mostrar sus propias ideas ya que todo ya estaría hecho, en cierto modo nos estarían dando las cosas hechas y nosotros no tendríamos que hacer nada, por lo que no, no estaría bien el que todos hiciéramos lo mismo porque así no explotas las cualidades personales que hacen especiales a cada persona.

Aquí os dejo el enlace de dicho artículo:

http://naukas.com/2013/05/22/por-que-se-sincronizan-los-metronomos/

CLASE 17 Y 18 DICIEMBRE

He hecho esta unión ya que en ambas clases estuvimos viendo como hacer ejercicio practicando en GEOGEBRA y WIRIS ya que tenemos examen mañana dia 21 de diciembre por parejas y en el ordenador.

El 18 hicimos uno de los problemas del exámen que previamente nos había mandado para casa que no pudimos terminar en clase y terminé en casa, después vi la solución y estaba bien: (os pongo lo que nos mando el ya que la mia esta en papel) 

El resto de los ejercicios los subiré uno de estos días ya que ahora no me da tiempo.

                          

CLASE 15 DICIEMBRE

Hoy en clase hemos estado hablando de las ecuaciones trigonométricas, tenemos 4 tipos que explicaré con ejemplos:

1. Ecuaciones del tipo una función trigonométrica igualada a una constante:                                x1=15º+k·180º    x2=45º+k·180º  las soluciones tras 1 giro son: 15º,45º,195º,225º
2. Ecuaciones que hay que factorizar: x1=90º+180ºk    x2=210º+360ºk   x3=330º+360ºk las soluciones tras el 1 giro son:90,210,270,330
3. Ecuaciones en las que las razones trigonométricas se expresan en función de una sola: x=0.90,180,270,360,450... de las que son válidas: 90º,450º,360º...     x1=360ºk   x2=90º+360ºk
4. Ecuaciones donde aplicamos los teoremas de la adición: estos teoremas son más faciles ya que solo hay que emplear los distintos teoremas de la adición que hemos ido aprendiendo.

CLASE 14 DICIEMBRE

Continuando con las razones trigonométricas vamos a hablar de las razones trigonométricas del ángulo doble y del ángulo mitad y las transformaciones de sumas de 2 razones en productos:
1.- Ángulo doble:
      - Sen 2a= sen (a+a)= sen a·cos a+ sen a·cos a= 2sen a·cos a
      - cos 2a= cos (a+a)= cos a·cos a- sen a·sen a=
      - Tg 2a= tg (a+a)= 
   En la actualidad utilizamos las siguientes expresiones derivadas de cos 2a:
        · cos 2a= 
        · cos 2a= 

2.- Ángulo mitad: partiendo del cambio de incógnita 2A=a y A=a/2
      - Cos 2A=
                      
                      
      -Cos 2A=
                     
                     
       - Tg a/2=se obtiene mediante el cociente:
                     


Transformaciones de sumas de 2 razones en productos:
Esto se hace porque es mas sencillo operar con productos a operar con sumas porque los productos se pueden simplificar en cambio las sumas no:
Transformaciones senos:
Partiendo de las fórmulas: sen (a+b)= sen a·cos b+cos a ·sen b y sen (a-b) sen a·cos b+sen b·cos b
1. sen (a+b)+sen (a-b)= 2sen a·cos b
Hacemos cambios de variable a+b=A y a-b=B
a=(A+B)/2 y b=(A-B)/2
sen A+sen B= 2sen (A+B)/2· cos  (A-B)/2
2. sen(a+b)-sen(a-b)= 2sen b·cos a
Con los anteriores cambios de variable queda:
sen A-sen B= 2cos (A+B)/2· sen  (A-B)/2
Transformaciones cosenos:
Partiendo de las fórmulas: cos (a+b)=cos a·cos b+sen (-a)·sen b y cos (a-b)=cos a·cos b+ sen a·sen b
1. cos (a+b)+cos(a-b)= 2cos a·cos b
Con los cambios de variable anteriores:
cos A+cos B= 2cos (A+B)/2· cos (A-B)/2
2. cos (a+b)-cos(a-b)= -2sen a·sen b
Con los cambios de variable anteriores:
cos A-cos B= -2sen (A+B)/2· sen (A-B)/2

MAPA TEMPORAL DE LOS MATEMÁTICOS

Aqui como nos pidió nuestro profesor pongo el mapa de los matemáticos que subí en una de las entradas anteriores:

Se sobresale un poco pero si lo hago más pequeño no se va a ver bien.

CLASE 11 DICIEMBRE

Hoy en clase hemos comenzado un nuevo tema también de trigonometría y comenzamos hablando de los teoremas de Adición que son:

1. Seno de la suma de 2 ángulos
2. Coseno de la suma de 2 ángulos
3. Tangente de la suma de 2 ángulos
4. Seno de la resta de 2 ángulos
5. Coseno de la resta de 2 ángulos
6. Tangente de la resta de 2 ángulos

1.- Seno suma 2 ángulos: usando el triángulo de la imagen podemos escribir que

 sen (a+b)=AR+RP=CB+RP Calculamos la medida de los segmentos CB y RP

CB= sen a·cos b         porque:

sen a=CB/OB=> CB=OB·sen a

cos b=OB/1=> OB=cos b

RP= cos a·sen b

cos a= RP/PB=>RP=PB·cos a

sen b= PB/1=> PB= sen b

sen (a+b)= sen a·cos b+cos a ·sen b

2.- Coseno suma 2 ángulos: Para ello necesitamos las relaciones que difieren 90º y la expresión anterior.

cos (a+b)= sen [90º+(a+b)]= sen [(90º+a)+b]= sen (90º+a)· cos b· sen a·cos (90º+a)=

cos a·cos b+sen (-a)·sen b

3.- Tangente suma 2 ángulos: usando las dos fórmulas de arriba hacemos el cociente entre sen y cos:

tg(a+b)=sen(a+b)/cos(a+b)=sen a·cos b+cos a ·sen b/cos a·cos b+sen (-a)·sen b

4.- Seno resta 2 ángulos: Sería como la anterior expresión (sen (a+b)) pero en vez de haber un + ponemos un -:

sen (a-b)= sen a·cos b-cos a ·sen b

5.- Coseno resta 2 ángulos: 

cos(a-b)= cos[a+(-b)]= cos a ·cos (-b) -sen a·sen (-b)= cos a·cos b+ sen a·sen b

6.- Tangente resta 2 ángulos: 

tg (a-b)=sen (a-b)/cos(a-b)=sen a·cos b-cos a ·sen b/cos a·cos b+ sen a·sen b=

=tg a-tg b/1+tg a·tg b

CLASE 10 DICIEMBRE

Hoy en clase hemos terminado el tema:
Para terminar la 1 parte de trigonometría acabamos con la resolución de triángulos cualesquiera y la expresión del área de un triángulo:
Para la resolución de estos triángulos se tendrán en cuenta las relaciones entre estos elementos:

1. La suma de sus ángulos es 180º.
2. Teorema de los senos.
3. Teorema del coseno.

Un triángulo queda definido cuando se saben tres de sus elementos excepto el caso de los ángulos.

EJ: conocemos dos lados y el ángulo comprendido entre ellos: b= 7m  c= 10m y A= 40º

  

Para la resolución de este ejercicio usamos el teorema del coseno:

a=

Con estos datos hallamos los dos ángulos:

Expresiones área de un triángulo: 

S=bh/2

Utilizando h en uno de los triángulos, usamos la expresión del valos del seno de la figura anterior:

sen A= h/b y poniendolo en la fórmula del área de un triángulo:

S=1/2·a·c·sen B

Fórmula Herón: es una fórmula que es conocida por usarse para el cálculo del ára de un triángulo del que solo conocemos los lados:

    donde p es el semiperímetro que calculamos con la suma de los lados entre 2.

MATEMÁTICOS/FILÓSOFOS ANTIGUOS

Aqui pongo una actividad propuesta por nuestro profesor:

Tales de Mileto 625ac-547ac astrónomo griego y trigonometría
Anaximandro Mileto 610ac-546ac astrónomo griego
Pitágoras de Samos 570ac-469ac astrónomo griego
Filolao de Tarento 470ac-385ac  astrónomo italiano
Eudoxo de Cnido 390ac-337ac astrónomo griego
Aristarco de Samos 310ac-230ac astrónomo griego
Eratóstenes de Cirene 276ac-194ac astrónomo italiano
Apolonio de Perga 262ac-190ac trigonometría Grecia
Hiparco de Nicea 190ac-120ac trigonometría Turquía
Menelao de Alejandría 70dc-140dc astrónomo Alejandría
Claudio Ptolomeo 90dc-168dc astrónomo Alejandría



(no se como girar la fotografía...)

REFLEXIÓN (¿EXISTEN LOS MALOS PROFESORES?)

Tras leer el artículo que más tarde os pondré he llegado a la conclusión de que en cierto modo los alumnos nos solemos acordar más del profesor que más nos exige que del que tiene menos carácter con nosotros. Este profesor que por así decirlo nos exige tiene sus métodos de hacer las cosas y muchas veces las maneras de hacernos aprender son muy diversas en incluso a veces muy divertidas como puede ser el caso de la creación de este blog que es una manera distinta de hacer las cosas de matemáticas. En mi opinión no existen profesores buenos y profesores malos, existen profesores mas exigentes y menos exigentes, porque esta distinción al igual que la mía es dependiendo de los distintos puntos de vista de los alumnos porque también depende de la asignatura que nos imparta este profesor no podemos comparar al profesor de lengua con la de biología, son asignaturas distintas y habrá métodos diferentes para ambos profesores. 

En conclusión según criterios podrá haber profesores buenos y profesores malos, exigentes y no exigentes, pero es lo que nos ha tocado a cada uno en clase, por lo que hay que estudiar e intentaer asemejarse lo más posible a lo que pide el profesor.

REFLEXIÓN (ALUMNO EXITOSO)

Tras un tiempo pensando, ha llegado el momento de la reflexión de unos artículos que al final de la entrada os pondré sobre el trabajo en equipo y el buen alumno:
Pues dado el caso de que recientemente hemos hecho un examen grupal en grupos de 5 y 6 alumnos aprovecho la reflexión para dar mi opinión sobre este asunto y lo complemento con mi reflexión sobre un buen alumno, este examen ha sido una experiencia nueva, que en cierto modo nos ha ayudado de cara a nuestro futuro porque en cualquier empresa por muy bueno que seas si no sabes trabajar en equipo no te van a aceptar. Este trabajo en grupo fomenta el trabajo en equipo y el apoyo mutuo entre los participantes de ese grupo.
Para que un estudiante consiga el éxito necesita según Erica Belcher una serie de aptitudes que se basan sobre todo en el buen trabajo del estudiante y el aprovechamiento máximo del tiempo empleado siempre aprendiendo de nuestros errores y sin ninguna falta ni queja por nuestros errores porque de los errores se aprende!!
En el otro artículo que os pongo es una muestra más del trabajo en equipo que antes mencionaba, de manera mas cómica, como se expresa en el artículo cada uno tiene sus defectos pero en el trabajo en equipo esos defectos pueden ser de ayuda o incluso pueden desaparecer tras este trabajo grupal, en este artículo nos lo explica de manera muy comica con las herramientas de un carpintero, por separado no hacen mucho pero en conjunto hacen un mueble estupendo!!.

Estudiante exitoso:
http://www.ehowenespanol.com/estudiante-exitoso-cualidades-debes-como_156414/

Trabajo en equipo:
https://dametresminutos.wordpress.com/2015/08/26/el-taller-de-nuestras-vidas/

CLASE 4 DICIEMBRE

Hoy en clase hemos estado viendo los teoremas del seno y coseno:

T. SENO:

 

En el triangulo ABC trazamos la altura h con vértice en A obtenemos dos triángulos ABH y AHC

sen B= hc/c=>hc=c·sen B

sen C= hc/b=>hc=b·sen C 

c·sen B= b·sen C

Despejando: b/sen B=c/sen C y con esto deducimos que c/sen C=a/sen A

El teorema del resto afirma que en un triángulo cualquiera los lados son proporcionales a los senos de sus ángulos opuestos: b/sen B=c/sen C=a/sen A

T. COSENO: 

Dado este triángulo ABC hemos trazado la altura h correspondiente a C que divide AB en 2 segmentos con longitudes p y m. Dados los triángulos AHC y BHC  podemos escribir:


Tras esta gran fórmula os pongo la definición de este teorema: el cuadrado de un lado es igual a la suma de los cuadrados de sus lados menos el doble producto de ellos por el coseno del ángulo que forman.

CLASE 3 DICIEMBRE

Hoy en clase hemos continuado con la trigonometría y hemos visto el método para resolver triángulos rectángulos y usamos las siguientes relaciones entre T. rectángulos:

1. La suma de dos ángulos agudos es igual a 90º: A+B=90º 
2. Teorema de pitágoras: 
3. Razones trigonométricas sen, cos, tg: sen A=a/c=cos B                                                                  cos A=b/c=sen B   tg A=a/c  tg B=b/a

EJ: Para un triangulo rectánmgulo ABC conocemos los dos catetos b=28,7m y a=13,5m resuelve el triángulo (es el de arriba):

c= una que tenemos estos datos hallamos los ángulos:

tg A=a/b= 28.7/13.5=2.13  B= 64º 48' 31''

tg B=b/a=13.5/28.7= 0.47  C= 25º 11' 29'' 

Y las razones trigonométricas de un ángulo cualquiera, entonces para eso usamos la circunferencia goniométrica (circunferencia de radio 1 centrada en el origen de coordenadas: para ello tendremos que saber el signo del seno coseno y tangente en cada cuadrante: 

Asi para un ángulo & del primer cuadrante 0º < & < 90º:

sen &= AB/OB= AB/1= AB

cos &= OA/OB= OA/1= OA

tg &= AB/OA=CD/OC=CD/1=CD

Tambien hemos visto las relaciones entre las razones trigonométricas de cualquier ángulo y son:

1. 
2. tg &= y/x= sen&/cos&
3. 
4. 

CLASE 1 DICIEMBRE

Hoy en clase hemos comenzado a hablar de trigonometria y estuvimos hablando de las razones trigonométricas de un ángulo agudo, partiendo de un triángulo rectángulo al que se le pueda aplicar el teorema de pitágoras.

  cateto al cuadrado + cateto al cuadrado =hipotenusa al cuadrado
       x=a y=b c=hip

A partir de esto tenemos las razones trigonométricas de un ángulo agudo:
seno (sen)= cateto opuesto/ hipotenusa
coseno (cos)=cateto contiguo/ hipotenusa
tangente (tg)=cateto opuesto/ cateto contiguo o sen/cos
luego estan las inversas:
cosecante (cosec)=1/sen o hip/ cateto opuesto
secante (sec)=1/cos o hip/ cateto contiguo
cotangente (cotg)=1/tg o cateto contiguo/ cateto opuesto


Casos especiales: 0º, 30º, 45º, 60º, 90º:



Son casos especiales por que en la mayoría son cocientes de números irracionales.

EJERCICIOS EXAMEN (CORRECCIÓN)

El otro día hice una serie de ejercicios del examen que habíamos hecho en clase y ahora os pongo la corrección de los 5 ejercicios que hice:
EJERCICIO 7: ESTA BIEN.

EJERCICIO 10: ESTA BIEN, pero como en clase solo dimos es pi y el e el tercer número trascendental es el número e al cuadrado, porque el cuadrado de un número es equivalente a ese número por lo que el cuadrado de un número trascendente no deja de ser un número trascendente.

Nuestro profesor nos ha marcado la proposición contrarrecíproca y nos ha pedido su demostración:
Demostración: todo número (a) perteneciente a R es radical en una raíz porque todo número es igual a la raíz cuadrada de ese número elevado al cuadrado:.

EJERCICIO 21: ESTA MAL: hice mal RUFFINI porque x+11 si que es factor del polinomio:
 corrección el fallo esta en la suma -16+44=28 y no =18
                /    1             4             -81               -16          308                     
                /
                /
          -11/                 -11             77                  44       -308
                      1           -7              -4                 28           0

EJERCICIO 33: ESTA BIEN, pero no lo terminé, porque yo dejo la respuesta como: x1=1, x2= y x3= estas dos últimas soluciones no están mal pero se deben simplificar: x2= y x3=

EJERCICIO 39: ESTA BIEN, pero sobran GRÁFICAS, la única que es respuesta es la gráfica del 5x-5y=5, una equivalente es x-y=1 y la única gráfica que habría que poner es:

EJERCICIOS EXAMEN.

El día 26 de Noviembre tuvimos el examen trimestral grupal, mi opinión sobre este examen es realmente positiva ya que me parece una muy buena manera de fortalecer el trabajo en equipo (del cual hablaré en mi próxima entrada haciendo una reflexión). Tras ese examen nuestro profesor nos asignó 2 ejercicios para hacer bien y tener perfectamente hechos en mi caso son el 7 y el 33, yo subiré esos 2 y alguno más que me ha llamado la atención.

EJ 7 EXAMEN: ¿TODO NÚMERO RADICAL ES ALGEBRAICO? DEMUESTRA

Si, todo número racional es algebraico ya que toda fracción a/b es solución de la ecuación bx-a=0 siempre a y b pertenezcan a Z.
Ejemplo: 3x-4=0 ; 3x=4; x=4/3   (a=4, b=3)

EJ 33 EXAMEN: RESUELVE 

Primero observamos el polinomio, al ser de grado 3 sabemos que tiene 3 soluciones:
Usamos ruffini:
             
                /    16                   -12                 -5                       1                          
                /
                /
              1/                            16                   4                      -1   
                      16                    4                   -1                       0  
Una vez que ya sabemos la primera raíz (1) resolvemos la ecuación resultante mediante la fórmula:      

x1=1     x2=    x3=
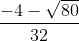
Haciendo la prueba del resto para comprobar si son soluciones he observado que si, si que lo son.
P(1)= 16 x 1 - 12 x 1 -5 x 1 + 1= 0
P(-0.4045)= 
P(0.1545)= 

EJ 39 EXAMEN:.- Dibuja la solución del sistema de ecuaciones 
Para hallar la solución de este sistema y dibujarlo, se basa sobretodo en dar valores a una de las incógnitas para hallar los valores de la otra.
5x-5y=5
x=0    y=-1
x=1    y=0
x=-1   y=-2

0x+0y=0
x=0    y=0
x=1    y=0
x=-1   y=0

Ahora la gráfica con ambas rectas

La solución de este problema es el punto que tiene ambas rectas en común: que en la representación es el punto C: x=1 y=0 S=(1,0)

EJ 21 EXAMEN: ¿ES DIVISIBLE  entre x+11

 

Para saber si es divisible intentamos resolverlo mediante ruffini.

 

                /    1             4             -81               -16          308                    
                /
                /
          -11/                 -11             77                  44        -198
                      1           -7              -4                 18          110 

No es divisible entre x+11 ya que el resto haciendo ruffini es 110 y no 0

EJ 10 EXAMEN: PON 3 EJEMPLOS DE NÚMEROS TRASCENDENTES
Primero voy a poner la definición de número trascendente: un número trascendente es aquel número irracional que no puede ser raíz de ningún polinomio de coeficientes enteros, por lo que un número trascendente no puede ser un número algebraico. Ejemplos: en clase hablamos del número pi y el número e, he buscado en internet un tercero ya que no me suena haber visto otro en clase: ln(a) siempre que a sea positivo, racional y diferente de 1 (logaritmo natural)