A lo largo de esta semana (lo que queda) iré poniendo los ejercicios resueltos del examen para casa.
Este es el examen:
Aquí tenéis el examen, a lo largo de esta semana intentaré poner las soluciones.
diario de César
el mundo matemático de 1 bach
miércoles, 15 de junio de 2016
martes, 7 de junio de 2016
TABLA DE DERIVADAS E INTEGRALES
Estos días en clase estamos dando de una manera un tanto rápida las integrales. Antes de esto pondré una tabla con las distintas derivadas que tenemos ya que va a ser muy útil de cara al examen de este jueves e incluso del jueves que viene.
La tabla será una imagen de internet la cual yo creo que es muy completa. Esta tabla también te muestra las derivadas de composiciones.
Pasamos a las integrales.
La integrales que vamos a estudiar este curso van a ser las integrales inmediatas y las casi inmediatas.
Una integral inmediata es aquella cuya función de la que parte es una de las derivadas de arriba (parte de la izquierda), es decir, son aquellas integrales que se van a dar al dar la vuelta a la derivada.
Una integral casi inmediata, es aquella cuya función va a tener un cambio de variable sencillo, usaremos la regla de la cadena en algunas ocasiones.
REGLA DEL CAMBIO DE VARIABLE:
Tenemos esta función, tipo integral y lo que vamos hacer es sustituir u(x) por t para transformar así la función casi inmediata en una inmediata.
Primero localizamos la u, en este caso  ya tenemos la variable t, por lo que pasaría a ser:
ya tenemos la variable t, por lo que pasaría a ser:

Volvemos a hacer el cambio de variable y quedaría:
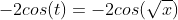
EJERCICIO EXAMEN PARA CASA:

Volvemos a hacer el cambio de variable y quedaría:
EJERCICIO EXAMEN PARA CASA:
RESOLUCIÓN
domingo, 5 de junio de 2016
CLASE 30-31 MAYO
En estas dos clases continuamos con las aplicaciones de las derivadas, en este caso dimos el estudio completo de una función.
Pasos:
1.- Dominio de f(x)
2.- Puntos de corte con los ejes:
- Corte con el eje y f(0)
- Ceros de f: f(x)=0
3.- Continuidad y asíntotas
- Verticales: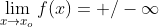
- Horizontales:
- Oblicuas:
4.- Monotonía y extremos relativos --> signo y ceros de f '
5.- Convexidad y puntos de inflexión --> signo y ceros de f ''
6.- Gráfica
7.- (recorrido, inyectividad...)
Para hacer un ejemplo he decidido hacer la función del ejercicio 5 del examen para casa:
Como hay un valor absoluto, voy a romper la función en trozos:
1.- Dominio: R-{0}
2.- Cortes con los ejes:
-Ceros de la función: 
- Corte con el eje y: NO TIENE, porque al sustituir el 0 se queda el 0 abajo.
3.- Continuidad y asíntotas:
- Verticales:

Hay una asíntota vertical en x=0
- Horizontales:
Hay una asíntota vertical en x=0
- Horizontales:
No hay asíntotas horizontales
- Oblicuas:
Hay asíntotas oblícuas.
4.- Monotonía y extremos relativos (signo y ceros de f ')

En el -1 vamos a tener un max relativo y en el 1 un mínimo relativo
5.- Convexidad y puntos de inflexión (signo y ceros de f '')
Habrá un punto de inflexión en el -1,4142
Respecto a la gráfica tengo mis dudas... por lo que mañana preguntaré y pondré como queda representada. Si teneis alguna duda dejadla en los comentarios.
lunes, 30 de mayo de 2016
CLASE 27 MAYO
Hoy en clase hemos continuado con las aplicaciones de las derivadas, hemos descubierto que una de las aplicaciones más interesantes son los problemas de optimización.
Haré uno en esta entrada para que veamos como se hace, según vayan pasando los días iré subiendo alguno más ya que resultan interesantes.
EJERCICIO:
Una empresa vinícola tiene plantadas 1200 cepas
de vid en una finca, produciendo cada cepa una media de 16 kg de uva.
Existe un estudio previo que garantiza que por cada cepa que se añade a
la finca, las cepas producen de media 0,01 kg menos de uva cada una. ¿Cuántas cepas se deben añadir a las existentes para que
la producción de uvas de la finca sea máxima?
Pasos:
1) Localizar la palabra máxima y así poner nombre a la función: P
2) Localizar la variable (suele estar en la pregunta)
3) Plantear la función y resolver:
P(x)=(1200+x)·(16-0,01)--> Dom P=R+
P'(x)=4-0,02x
Resolvemos esta función como si fuera una ecuación:
4-0,02x=0; x=200
200 es un máximo relativo ya que la derivada segunda de P es negativa. (P''(x)=-0,002)
Aparte de esto, también vimos como se hace el estudio completo de una función sin necesidad de hacer la gráfica:
ESTUDIO COMPLETO DE LA FUNCIÓN F:
1.- Dominio de f
2.- Puntos de corte con los ejes:
a) Ceros de f: resolviendo la ecuación
b) Corte con el eje y: f(0)
3.- Continuidad y asíntotas:
a) Verticales: 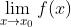
b) Horizontales:  y
y 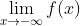
c) Oblicuas:  y
y 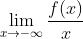
4.- Monotonía y extremos relativos de f relacionado con el signo y ceros de f '
5.- Convexidad y puntos de inflexión de f relacionado con el signo y ceros de f ''
6.- Gráfica de la función f
A partir de aquí, podéis estudiar el recorrido, inyectividad...
A lo largo de la semana publicaré los ejercicios que vaya haciendo, si tenéis alguna duda dejadla en los comentarios.
jueves, 26 de mayo de 2016
CLASE 24 MAYO
Hoy en clase continuando el tema de las asociaciones de derivadas hemos aprendido el método para hallar la convexidad de una función.
Convexidad de una función:
U=> convexa hacia arriba
Ej: de cóncava o convexa hacia arriba
Ej: de convexa hacia abajo.
Definición (geométrica): f se dice convexa hacia arriba en su dominio (puede ser también en un intervalo y en un punto) si la región superior determinada por su gráfica es convexa*.
*¿Qué es región plana convexa? con la definición de región plana, se dice que es convexa, cuando el segmento que une a dos puntos cualesquiera de dicha región este dentro de la misma.
Ejercicio: determinar cuales de las siguientes regiones son convexas:
Son convexas la 1,2,4,6. La 3 y 5 no porque como podemos observar podemos hacer un segmento que no esté en la región.
Propiedad: cuando f es convexa hacia arriba o hacia abajo las rectas tangentes van a estar por fuera.
Convexidad de la función afín:
Es convexa hacia arriba y hacia abajo.
Convexidad función: y= 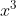
No es convexa en su totalidad, es convexa hacia arriba en el intervalo de [0,+∞] y convexa hacia abajo en el intervalo [-∞ ,0]
Observamos que en el 0 hay un punto de inflexión ya que hay un cambio de convexidad.
Proposición: Una función f es convexa hacia arriba <=> f ' es creciente
Una función f es convexa hacia abajo <=> f ' es decreciente
¿Un punto que es P.I de f <=>f ''=0?
De estas es cierta solo 1, es cierta => ya que siempre que f es un punto de inflexión la f ''=0
Ponemos un contraejemplo para ver que <= es falsa:
Cuando y=x y'=1 y''=0. esta derivada segunda será 0 en todo su dominio, y como se podrá entender no hay puntos de inflexión en todo su dominio.
Suscribirse a:
Entradas (Atom)








