CLASE 27 MAYO

Hoy en clase hemos continuado con las aplicaciones de las derivadas, hemos descubierto que una de las aplicaciones más interesantes son los problemas de optimización.

Haré uno en esta entrada para que veamos como se hace, según vayan pasando los días iré subiendo alguno más ya que resultan interesantes.

EJERCICIO:

Una empresa vinícola tiene plantadas 1200 cepas de vid en una finca, produciendo cada cepa una media de 16 kg de uva. Existe un estudio previo que garantiza que por cada cepa que se añade a la finca, las cepas producen de media 0,01 kg menos de uva cada una. ¿Cuántas cepas se deben añadir a las existentes para que la producción de uvas de la finca sea máxima?

Pasos:

1) Localizar la palabra máxima y así poner nombre a la función: P

2) Localizar la variable (suele estar en la pregunta)

3) Plantear la función y resolver:

P(x)=(1200+x)·(16-0,01)--> Dom P=R+

P'(x)=4-0,02x

Resolvemos esta función como si fuera una ecuación:

4-0,02x=0; x=200

200 es un máximo relativo ya que la derivada segunda de P es negativa. (P''(x)=-0,002)

Aparte de esto, también vimos como se hace el estudio completo de una función sin necesidad de hacer la gráfica:

ESTUDIO COMPLETO DE LA FUNCIÓN F:

1.- Dominio de f

2.- Puntos de corte con los ejes:

      a) Ceros de f: resolviendo la ecuación

      b) Corte con el eje y: f(0)

3.- Continuidad y asíntotas:

      a) Verticales: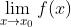  

      b) Horizontales:      y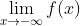  

      c) Oblicuas:          y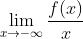    

4.- Monotonía y extremos relativos de f relacionado con el signo y ceros de f '

5.- Convexidad y puntos de inflexión de f relacionado con el signo y ceros de f ''

6.- Gráfica de la función f

A partir de aquí, podéis estudiar el recorrido, inyectividad...

A lo largo de la semana publicaré los ejercicios que vaya haciendo, si tenéis alguna duda dejadla en los comentarios. 

CLASE 24 MAYO

Hoy en clase continuando el tema de las asociaciones de derivadas hemos aprendido el método para hallar la convexidad de una función. 

Convexidad de una función:

U=> convexa hacia arriba

=> convexa hacia abajo

Ej: de cóncava o convexa hacia arriba 

Ej: de convexa hacia abajo.

Definición (geométrica): f se dice convexa hacia arriba en su dominio (puede ser también en un intervalo y en un punto) si la región superior determinada por su gráfica es convexa*.

*¿Qué es región plana convexa? con la definición de región plana, se dice que es convexa, cuando el segmento que une a dos puntos cualesquiera de dicha región este dentro de la misma. 

Ejercicio: determinar cuales de las siguientes regiones son convexas:

Son convexas la 1,2,4,6. La 3 y 5 no porque como podemos observar podemos hacer un segmento que no esté en la región.

Propiedad: cuando f es convexa hacia arriba o hacia abajo las rectas tangentes van a estar por fuera. 

Convexidad de la función afín:

Es convexa hacia arriba y hacia abajo.

Convexidad función: y= 

No es convexa en su totalidad, es convexa hacia arriba en el intervalo de [0,+∞] y convexa hacia abajo en el intervalo  [-∞ ,0]

Observamos que en el 0 hay un punto de inflexión ya que hay un cambio de convexidad. 

Proposición:  Una función f es convexa hacia arriba <=> f ' es creciente 

                      Una función f es convexa hacia abajo <=> f ' es decreciente 

                      

¿Un punto que es P.I de f <=>f ''=0?

De estas es cierta solo 1, es cierta => ya que siempre que f es un punto de inflexión la f ''=0

Ponemos un contraejemplo para ver que <= es falsa:

Cuando y=x y'=1 y''=0. esta derivada segunda será 0 en todo su dominio, y como se podrá entender no hay puntos de inflexión en todo su dominio.

CLASE 23 MAYO

Hoy en clase continuando con las aplicaciones de las derivadas, hemos aprendido un nuevo método que nos será muy útil en el ámbito del estudio de una gráfica.

MÉTODO DE BISECCIÓN:

Para resolver una ecuación en forma de función podemos hallar los denominados ceros de la función o hallando la antiimagen, pero ¿Qué es la antiimagen?

Antes, voy a poner un ejemplo de cuando sería necesario calcular esta antiimagen.

Ecuación: 2x+1                                 Función: y=2x+1 (resolver hallando los ceros)

ecuación +5x=3                             Función: y=+5x (hallar la antiimagen de 3)

La antiimagen es darle la vuelta a la imagen, es hacer lo que hacíamos con la función recíproca

A cada x le asociamos una y, lo que sería la imagen de x

A cada y le asociamos una x, lo que sería la antiimagen de y, 

¿Cuándo la antiimagen de y es 0?

Las de grado 1 no nos van a valer ya que son rectas y siempre va a haber un punto de corte ya que su recorrido va a ser de (-∞,+ ∞) 

Ahora vamos a ver que sucede con las de grado 0 y de grado 2:

En la de grado 0, como va a ser una función constante k, cualquier punto que no sea k, la antimagen va a ser 0

En la de grado 2: Lo haré con una gráfica:

El punto y, que no pertenece a la gráfica su antiimagen va a ser 0.

Una vez visto lo que es la antiimagen, pasamos al método de bisección:

Asociado siempre a las funciones polinómicas relacionadas con la continuidad.

El Método de Bisección, va muy ligado a 2 teoremas, el de Bolzano y el Teorema del valor medio de Darboux.

Según teorema de Bolzano, si fuera el de darboux en vez de 3 sería el 0.

Vamos a la función de antes: y=+5x, hallar la antiimagen de 3

La antiimagen de 3 va a ser 0,56

CLASE 20 MAYO

Hoy en clase hemos comenzado con el nuevo tema de las derivadas, con las aplicaciones de las derivadas.

Para una f cualquiera:

RELACIÓN ENTRE MONOTONÍA Y EXTREMOS DE F CON EL SIGNO Y CEROS DE F'

Proposición:

f crece en un cierto intervalo <=> f '>0 en un intervalo

f decrece en un cierto intervalo <=> f '<0 en un intervalo

¿Y si f '=0?

Si en un Xo f '(Xo)=0 se pueden dar 2 casos: (1 cierto y el otro no)

- Que eso implique que Xo sea un extremo relativo (FALSO) contraejemplo: La gráfica de la función

- La otra opción, que el extremo relativo implique que f '(Xo)=0

EJEMPLO: Estudia la monotonía de 

Para estudiar la monotonía, necesitamos el signo y los ceros, los cuales se van a resolver con una ecuación y una inecuación.

Con la ecuación vamos a hallar aquellos puntos en los que se va a cero la función derivada. 

Ec:  Los puntos en en los que la función derivada se va a hacer cero, son -1,55 y 0,22

Para hacer el estudio del signo, con la inecuación, vamos hacer una recta y el estudio del signo.

Al observar la inecuación podemos ver que se trata de una parábola por lo que podemos ver en puntos va a crecer y en cuales decrecer:

CLASE 16 MAYO

Hoy en clase hemos seguido con el tema de las derivadas, hemos visto las derivadas sucesivas, es decir, derivadas n-ésimas.

Lo que queremos hacer es encontrar la derivada n-ésima, mediante el principio de inducción (visto al principio de curso)

Ejercicio:

 

  

Sospechamos (hipótesis por inducción) que:

Tras esta sospecha tenemos que hacer la llamada demostración por inducción.

n=1

Si la derivada n-ésima es    la derivada n+1 debería ser la derivada de la derivada n-ésima:

Aparte de este ejemplo, hay más que quedaron como tarea que intentaré hacer este fin de semana ya que ahora no dispongo de tiempo. Si alguien tiene alguna pregunta, que no dude en dejarla en los comentarios

INDICE TRABAJO

Aquí os propongo un índice sobre este tema "Trasmisión del conocimiento: difusión científica", que dentro de unos días estudiaremos, y en mi caso junto a otros compañeros crearemos un índice global, válido para todos mis compañeros.
Como todo trabajo, comenzaré con la introducción y algunas palabras clave o "keywords".

1.- Introducción
     1.1 Palabras clave
     1.2 Prólogo

2.- Trasmisión del conocimiento
     2.1 ¿Qué es?
     2.2 Trasmisión del conocimiento a lo largo de la prehistoria
            2.2.1 Egipto
            2.2.2 Mesopotamia
     2.3 Trasmisión del conocimiento a lo largo de la historia
            2.3.1 Grecia
            2.3.2 Roma
            2.3.3 Edad Media
            2.3.4 Edad Moderna
            2.3.5 Edad Contemporánea

3.- Difusión científica:
     3.1 ¿Qué es?
     3.2 Medios de difusión científica:
            3.2.1 Signos y símbolos
            3.2.2 Lenguaje
                     3.2.2.1 Musical
                     3.2.2.2 Artístico

                     3.2.2.3 Gestual

                     3.2.2.4 Hablado

4.- Conclusión

5.- Bibliografía y fuentes

EXAMEN DERIVADAS EJ 10

Después de un rato, lo tengo hecho.

Ejercicio 10:

EXAMEN DERIVADAS (2)

Ahora os pongo la 2 parte de este examen. Voy a poner hasta el 9, en el ejercicio 10 me ha surgido un problemilla que espero resolver sin mas demora esta tarde.

Ejercicio 6:

Ejercicio 7:

Ejercicio 8:

Ejercicio 9:

EXAMEN DERIVADAS (1)

Ahora os pondré las primeras 5 derivadas.

Siento el método de presentación de este examen, ya que no lo voy a hacer en latex, sino que lo pondré en fotos.

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

CLASE 12 MAYO

Hoy en clase no hemos conseguido comenzar un tema nuevo ya que teníamos que finiquitar ciertas proposiciones y otros conceptos no del todo repasados, hablando sobre todo de algo que no habíamos dado y es la función implícita, ya vista en las ecuaciones de la recta.

DERIVADA DE LA FUNCIÓN IMPLÍCITA:

Ej:    la y función implícita de la x.

Para ello hablaremos del Teorema fundamental de la función implícita (Hay una muy buena explicación en el enlace que os he puesto abajo en la página 141)

La función implícita esta unida al tema de las cónicas y en este caso (el de abajo) vamos a tener una circunferencia, tendremos que coger la parte de arriba ya que para que sea una función tiene que haber una correspondencia en la cual a cada y se le hace corresponder una x.

 derivamos: 

Otro ejemplo:

     y'??

(INCISO): Vamos a hacer unos ejercicios de la derivada de (kf)':

1.- 

2.- 

3.- 

4.- 

Volviendo a la derivada de la función implícita:

Ejercicio: hallar y' de la función 

Una vez hallada, halla la ec de la recta tangente en x=1

y-yo-y'(xo)(x-xo)=0

La recta y=0 va a ser una recta horizontal paralela al eje x



Si tenéis alguna duda dejadla en lo comentarios.

(Enlace teorema de la f. Implícita. OS RECUERDO PAG 141)
apunte_cvv_felmer-jofre.pdf