![P(x)\in{\mathbb{Z[X]}}](http://rinconmatematico.com/latexrender/pictures/11a6ce56c25b3ee9bcf72f0826a347f3.png "P(x)\in{\mathbb{Z[X]}}")
Donde
raíz de P(x) 
Probamos si
se puede hacer, y descubrimos que no ya que un divisor de a0 no tiene porque ser raíz de ese polinomio.Proposición contrarrecíproca:
si a no es divisor de a0, a no es raíz de P(x)Ej: Factoriza P(x)=
Podemos hacerlo de dos maneras:1) sustituir todos los divisores del termino independiente(+/- 1, +/-2, +/-3, +/-6) en P(x):
P(1)=...........
2) Usar Ruffini con los divisores (solo tomaremos como posibles raices +/-1 y +/-2 ya que el polinomio se puede simplificar entre 3):
|
|
3 6 -3 -6
|
|
|
|
|
|
|
|
1
|
3 9 6
|
|
|
3 9 6 0
|
P(x)=(x-1)(
) ahora resolvemos el polinomio resultante:
) ahora resolvemos el polinomio resultante:![\frac{-9\pm\sqrt[2]{81-4\cdot{6\cdot{3}}}}{6}=\frac{-9\pm\sqrt[2]{9}}{6}](http://rinconmatematico.com/latexrender/pictures/8ff8a8981b074874c5d5a7f886351cc4.png "\frac{-9\pm\sqrt[2]{81-4\cdot{6\cdot{3}}}}{6}=\frac{-9\pm\sqrt[2]{9}}{6}")
x1= -1 x2=-2
Factorización: 3(x-1)(x+1)(x+2)
El polinomio (x-1) o (x+1) o (x+1) son polinomios que no se pueden reducir más, es decir, son polinomios irreducibles.
Ejercicio: Factorizar 
Pues a simple vista se puede observar que este polinomio no tiene solución real porque no se puede hacer la raíz cuadrada de un número negativo. Por lo que la factorización sería: ya que este polinomio es un polinomio irreducible.
ya que este polinomio es un polinomio irreducible.
Ejercicio: Factorizar 
Tambíen con este se puede observar que no tiene raíces enteras ***
Podemos intentar resolver: 
no es un numero real.
no es un numero real.
Pero esto nos puede hacer pensar, porque ambos son cuadrados.....
os preguntareis de donde sale el -4x al cuadrado y es porque si queremos igualar esta identidad notable con lo que tenemos al igual que se suma 4x a la 2 se tiene que resta 4x a la 2. Mañana os subiré la resolución de esta ecuación ya que por mucho que lo he estado intentando no me ha salido nada "lógico"
*: Vamos a hacer una generalización:
Partiendo de que P(x)=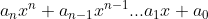
(an no puede ser igual a 0) y ![P(x) \in{\mathbb{R}[x]}](http://rinconmatematico.com/latexrender/pictures/32d3e342e46549b4fa4f4f2d610b0187.png "P(x) \in{\mathbb{R}[x]}")
sus raíces son: x1, x2,.... xn y su factorización= an (x-x1)(x-x2)....(x-xn).
sus raíces son: x1, x2,.... xn y su factorización= an (x-x1)(x-x2)....(x-xn).
Tenemos un problema para sacar las raíces:
1) La dificultad para encontrarlas
2) que P(x) no tenga raíces
Por lo que ampliamos 
donde C es un grupo que lo engloba todo mas los números complejos y ahora usamos el Teorema Fundamental de la Álgebra:
donde C es un grupo que lo engloba todo mas los números complejos y ahora usamos el Teorema Fundamental de la Álgebra:
Todo polinomio de grado n tiene n raíces complejas.
No hay comentarios:
Publicar un comentario