y nos ha pedido factorizarlo por lo que hacemos esto:![\frac{-7\pm\sqrt[2]{7^2-4\cdot{6}\cdot{-3}}}{12}=\frac{-7\pm\sqrt[2]{49+72}}{12}=\frac{-7\pm11}{12}](http://rinconmatematico.com/latexrender/pictures/a0e71a12fcb2dc2f3fc859416115ff9e.png "\frac{-7\pm\sqrt[2]{7^2-4\cdot{6}\cdot{-3}}}{12}=\frac{-7\pm\sqrt[2]{49+72}}{12}=\frac{-7\pm11}{12}")
x1=
x2=
Ahora sabemos que x-1/3 es divisor/factor de P(x). Aunque sepamos la otra raíz, vamos ha hacer que no nos la sabemos y solo tenemos 1 que es 1/3, vamos a hallar la otra mediante Ruffini:(es un ruffini raro porque no he encontrado otra manera de hacerlo)
6 7
|
-3
|
|
1/3 |
2
|
3
|
6 9
|
0
|
Con esto llegamos a la conclusión de que P(x)= = 
ahora sacamos factor común y nos queda: 
que es la factorización.
= ahora sacamos factor común y nos queda: que es la factorización.
PROPOSICIÓN:
x1 y x2 raíces de P(x) 
)
)
Luego hemos estado hablando otra vez de las raices de un polinomio:
(Definición): a es raíz de P(x)
PROPOSICIÓN:
![P(x)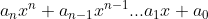\in{\mathbb{Z[X]}}](http://rinconmatematico.com/latexrender/pictures/11a6ce56c25b3ee9bcf72f0826a347f3.png "P(x)\in{\mathbb{Z[X]}}")
P(x)= 
donde 
raíz de P(x) 
( / la barra esta es que a es divisor de a0)
raíz de P(x) ( / la barra esta es que a es divisor de a0)
No hay comentarios:
Publicar un comentario